たし算とひき算の教え方‐2
たし算とひき算の教え方‐1からの続きです。まだ読んでいない方はたし算とひき算の教え方‐1をご覧ください。
⑥文章題 について〈その1〉
★子どもたちは文章題が苦手?!
よく、「計算はできるのに文章題が苦手で…」という話を聞きます。
問題を読んで正しい式が作れない子、文章題は苦手だとそっぽをむく子は大勢います。
【たし算・ひき算 間違い例】
①わなげをしました。
1かいめは 4つ、2かいめは 3つ はいりました。
あわせて いくつ はいりましたか。
しき 1+4+2+3=10
こたえ 10つ
②450円で えほんをかって 500円 はらうと おつりはいくらですか。
しき 450-500=50
こたえ 50円

たし算・ひき算の文章題は、大人にとってこれほど簡単なものはない! というふうに思えるのですが、まだまだ人生経験に乏しい子どもたちは ちょっとひねった問題になると 途端に混乱してしまいます。
上の間違い例のように、文中に出てきた数字を順番に書いて「+」か「-」でつないですませる場合も多いのです。「問題をよく読まないからでしょ!」なんてつい責めてしまったり…。でも本当に、よく読めば解けるのでしょうか?
苦手の原因を、「読解力不足」と考える人もありますが、読書好きの子どもが得意かと言えばそうとも限りません。語彙(ごい)の貧弱さ、イメージ力の乏しさもあるけれど、主要な原因は、「演算の意味」がしっかり教えられていない ことにあります。また「量」になじんでいないこと、たし算・ひき算ができる量かどうかの区別の指導が軽く扱われていること も影響しています。
これまで何度もお話ししてきましたが、最初に演算を学ぶ上で大切なのは、どんな時に使う計算か、その意味をわかっているかどうか ということです。おさらいをしますと、
あわせた数を出すのが 「たし算」 で、 残った数を出すのが 「ひき算」 でした。
これが最も基本となる考え方になります。
この基本の考え方で、一番典型的な場面を例にして、たし算、ひき算とはどういうものかを学び、計算を習熟した後、いろいろな種類の問題を指導していきます。
実はたし算ん・ひき算はいろいろな型に分類することができます。教える側の大人は、そのことを知った上で子どもの状況に合わせた与え方をする必要があります。
*たし算の種類
たし算の基本は「あわせていくつ?」なので、最初は次のような問題で考えます。

本物のみかんを手に持って目の前のお皿にバサッと入れてみます。小さい子どもたちは実物やタイルを動かす操作活動を通して思考力が育ちます。最初に「合併型」を持ってくるのは、操作をしやすく子どもたちに理解しやすい からです。
続いて、同じ「あわせていくつ?」になるのですが、違う種類のものをあわせています。

男の子3人と女の子1人で何人か?といった問題に「男の子と女の子はたせない」とひっかかる子どももいます。子どもは全部で何人かと聞くことで納得できるでしょう。
次は、時間的経過を伴うたしざんです。


体重が増えた、赤ちゃんが生まれて人口が増えた、といった場面もこの型になります。
合併型の①と②は、たす順番を変えても成り立ちますが、③の場合は成り立ちません。
これらが1~2年生でおもに扱われるたし算です。このほかに、一方より多い量を求める場合のたし算もあります。

この場合は、シールが増えたわけではありません。兄の分は、弟の数を兄の数に置き直して3を加えることで出てくるので、一段階、難しくなります。
また、弟が5枚、兄は8枚なので、シールの数は全部で13枚存在していますね。
ここまでは、ものの多さを表す数(集合数)どうしのたし算でした。今度は、○番目 のような順番とか位置を表す数である「順序数」のたし算になります。 順序数は、例えば1等と3等をあわせても4等にならないように、いつでもたし算ができる数ではありません。
けれど、次のような例ではたし算で答を求めることになります。

順序数はいつでもたし算ができるわけではないので注意が必要です。
このタイプはたし算の学習のずっと後の方で学ぶのが良いと思います。 このように、一口にたし算といってもいろいろな種類があることがわかりますね。
けれど、あらゆるたし算は「あわせていくつ?」という合併型にもどして説明することができるので、「合併」をたし算の基本と位置づけているわけです。
*ひき算の種類
ひき算の基本は「のこりはいくつ?」なので、最初は次のような問題で考えます。

ひき算においては、実物やタイルを動かす操作活動がしやすい「除去」が最もわかりやすい例です。 取り除いた残りを尋ねているので、ひき算のイメージに合っています。
続いて、求残に近いけれども実際に減ったわけではないという場合です。

たし算②の逆にあたります。

上の二つはさほど難しくありませんが、次の差を求めるものは一段と難しくなります。

「女の子から男の子はひけない…」とひっかかる子どもがいます。
この場合は、女の子と男の子に手をつながせて1対1対応させます。すると、手をつなげなかった女の子が出てくるので女の子の方が多いとわかります。「女の子全員」から、「男の子と手をつないだ女の子」をひいて「残りの女の子の数」が出てきます。「のこりはいくつ?」のひき算の意味にも合うわけです。
こうしたていねいな指導が必要なので①と②のタイプが十分できるようになったずっと後に③の求差型を入れるべきです。けれど教科書では求残型のすぐ後に差を求めるひき算が出てくるので混乱の原因になっています。


比べるものが異なる種類になると更に難しくなります。こたえ の助数詞にも注意が必要です。
このほかに、たし算④に対応して、一方より少ない量を求める場合のひき算もあります。

この場合も、シールは減りません。二つの量の「差」がわかっていることになります。
そしてやはり弟が5枚、兄は8枚なので、シールの数は全部で13枚存在していますね。
ひき算の場合も、次のような例では「順序数」のひき算で答を求めることになります。

順序数はいつでもひき算ができるわけではないので注意が必要です。
このタイプはひき算の学習のずっと後の方で学ぶのが良いと思います。
このように、ひき算の種類もさまざまです。けれどやはり、ひき算の基本は、「のこりはいくつ?」という求残型であると言えます。
⑦文章題について〈その2〉
★「文章題」の指導で大切なことは?
「文章題」で大切なのは、
何と何がわかっていて、
何を求めるときにどんな式をたてるのかです。
たし算・ひき算を初めて学ぶ子どもたちに対しては、できるだけ具体物とかタイルを使ってくり返し操作(合併と除去)し、経験させます。そしてそれらを、さんすうの言葉でどう表すのか を、折にふれ示していくと、文章題はできるようになります。
はじめて習うところは、まず、 基本の考えをしっかり定着させる ことが大切です。それは後ほど習う「かけ算」「わり算」についても同じです。
ところで、よく文章題を教えるときに、「もらった」「多い」などの言葉があればたしざん、「食べた」「帰った」などはひき算、などと教えている人を見かけますがどうでしょう? 次の問題を考えてみてください。

「もらった」や「ぜんぶで」など、たし算を連想させる言葉が入っていますが、求める式はひき算になります。それに問題のお話が最初に持っていたみかんより増えているので、「たし算」と勘違いする子どもは多いのです。「3+7=10」としたり「4+3=7」とする間違いがよく見られる問題で、一般には「逆思考」問題とも呼ばれています。

今度は「出ていった」の言葉が入っていますが、求める式はたしざんになりました。そしてお話の内容では車の数がはじめより減っているので、たし算で求めることに違和感を覚える子どもも多いのです。「出ていった3台に駐車場へ帰ってきてもらうとどうなるかな?」と言って元の状態に戻してみたら気がついてくれます。
大人と違い、子どもたちはちょっとしたところでひっかかりを抱いてわからなくなっている場合があります。どこがわからないかと聞いても、低学年の子どもはうまく言葉で説明できません。具体物や絵で説明したり、ストーリーを追ってわかっていることを一緒に確認したり、数字を易しいものに変えて考えさせたり、どこでひっかかりを持っているかを見つけてあげて、教える側が適切な助言をすることでわかってくれることもあります。
いままで見てきたように、1年~2年生くらいでいろいろなタイプの問題が出てきますので、子どもの発達段階によっては途方もなく難しくなる ということをどうか知っておいて下さい。文章題の力をつけようと買ったドリルで子どもが混乱して自信をなくすケースは意外と多いので気をつけてあげましょう。
★「文章題」を解く力が育つために…
文章題を解く力をつけるために、式を与えてその式になる文章題を子どもたちに作らせることがあります。「問題作り(算数のお話作り)」と呼んでいて、基本的な演算の意味がわかっているかどうか確かめる時には有効です。
けれども次のような例もみられます。
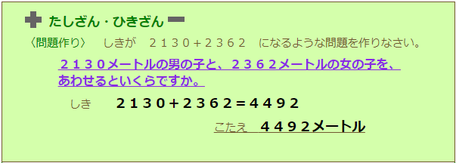
これは極端な例ではありますが、子どもたちの中には、現実の世界ではあり得ない数値を設定してしまったり、たし算できないもの、たし算しても意味がないものをたしてみたりということがしばしば見られます。たとえ計算の答が正しく導き出せたとしても、たし算・ひき算がわかっているとは言えません。量や単位の感覚が現実とかけ離れている子ども、生活の中で量や単位にふれあえていない子どもたちが多いように思います。
計算が正しく早くできても、それだけでは役に立ちません。計算なら電卓の方がよほど早くて正確です。算数が役に立つためには文章題が解けることが大事です。文章題は身の周りの問題を数学的に解決するものだから、生活経験や遊びから学び取るものが大きい のです。
大いに遊び、そして量の世界とも親しみ、感覚を養って算数に強くなりましょう。
*「たし算・ひき算」の文章題、大人も考えてみよう!~ 解答例&解説つき ~
いつもは子どもに「問題をちゃんと読んだらわかるでしょ!」なんて言っているけど、
文章題ってやっぱり、面倒で た~いへん!
簡単! 楽勝!…なんて思っているお父さん、お母さん、子どもの気持ちになって、大人も、たし算・ひき算に取り組んでみませんか。こんな問題、やってみよう!(これは大人向け問題です。小さい子どもさんにさせて困らせないでね!)
【たせるかな? たせないかな?】
①校内マラソンで私は49位、正さんは27位でした。正さんがゴールしてから私がゴールするまでの間、何人の人がゴールしましたか?
②超大作映画を見に行きました。映画は、午前10時50分に始まって、3時間20分かかります。おわるのは、午後何時何分ですか?
③1秒間あたり10mの速さで走る電車と、1秒間あたり15mの速さで走る電車をつなぐと、1秒間あたり 10+15=25m の速さで走る電車になりますか?
④1分間あたり40mの速さと、1分間あたり60mの速さをたして、速さが100m/分になることがあるでしょうか?
⑤40℃のお湯に50℃のお湯を加えると、40+50=90℃ のお湯になりますか?
⑥今年の10月1日の北九州市の最高気温は18℃で、去年の同日の最高気温は16℃でした。あわせると何℃ですか?また、この問いに意味があるでしょうか?
⑦9℃+12℃=21℃ が成り立つような文章題を考えて下さい。
⑧全商品30%引きと書いてある店で、2つの商品を買うと30+30=60%引きになりますか?
⑨体重が32㎏の男の子がいます。二つのヘルスメーターを並べて置き、二つに片足をのせて上がり、ピタッと止まったときにそれぞれのメモリをよみました。すると、右のヘルスメーターは19kgを指していました。このとき、左のヘルスメーターは、32-19=13㎏ を指すでしょうか?
⑩500gの水の中に100gの砂糖を入れて溶かしました。全部で何gになりますか?また、500gの水に100gの木を浮かべました。全部で何gになりますか?今度は、500gの水に100gの氷を浮かべました。溶ける前と溶けた後でそれぞれ何gになるでしょう?
⑪油の量は重さ(g)で表示してあるのに、しょうゆや牛乳は体積(mLやL)で表示してあります。なぜでしょう?
解答例と解説
問題を解いてみていかがでしたか? どうするのかなぁ?? と悩まれたものもあったのでは?!
では、1問ずつ、解答例をあげて解説をします。
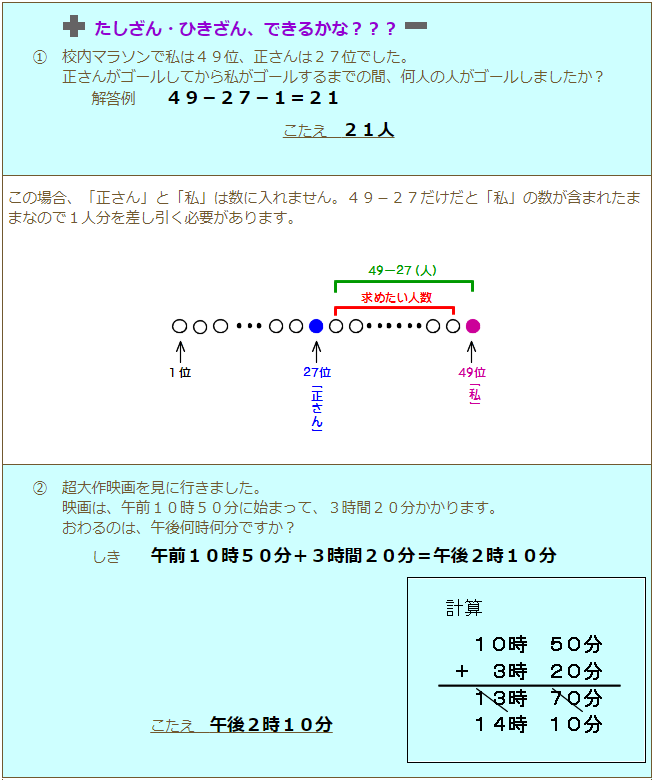
時刻に時間をたす問題です。時間の計算では単位をそろえることが大切です。60分でくり上がるので難しいですね。おまけに、午後何時何分かと聞いているので答えの書き方には注意が必要です。

③ 速さは自由にたしざん・ひきざんができない量です。この場合はたしざんは成立しません。
④ 速さのたしざんが成り立つ例です。他に、川の流れと船の速度などで出題されるケースもあります。

⑤温度も自由にたしざん・ひきざんができない量の一つです。皆さんも経験して知っている通り、この場合のたしざんは成立しません。
⑥気温も同じく自由にたしざん・ひきざんはできませんが、平均気温などを出す場合の過程でたしざんをする意味はありますね。
⑦気温に温度差をたす問題の例です。

⑧もしこんなたしざんが成立したら、商品が無料になったり、逆にお金をもらえてしまうこともありえますね! 2つの商品を買ったとき、a円の30%引き と b円の30%引きになるので、合計金額(a+b)円の30%引き になります。

⑨ 「重さ」という量は目で見ただけではわかりずらいですね。それゆえ、自由にたしざん・ひきざんができると考えられない子は多いです。実際に体重計でこのような実験をしてみるといいかもしれません。
⑩ こちらも全て重さは600gになります。砂糖が水の中に溶けて見えなくなってしまうと「重さ」までなくなったと考える子どもは案外多いのです。浮かんでいる木も、水中を動いている魚も重さはちゃんと存在しているので、たしざんが成り立ちます。「重さ」には「加法性」があることを子どもたちには知ってほしいと思います。ちなみに「かさ」(体積)はというと、「1リットル+1リットル=2リットル」にならない場合があります。
⑪ 同じ油の重さでも、夏と冬とでは体積が変わるので、油はグラム表記になっています。ご家庭で、油の重さ表示と、ジュースなどの表示を見比べてみましょう。こういった身近なものの表示を調べてみると、子どもたちにも量感覚や単位の感覚が育ちやすいのではないかと思います。
いずれも、生活経験が重要 ということです。
