たし算とひき算の教え方‐1
「たしざん・ひきざん」を「水道方式」ではどのように教えていくのか、教材や資料を例にあげて紹介していきます。
①たし算・ひき算って どんな時に使うの?
★たし算・ひき算の意味
0~9(または0~5)までの「数」がわかると、この範囲での たし算・ひき算 ができますね。
ところで、たし算って どういうときにする(できる)でしょう?
次の①~⑩番の問題を ちょっと考えてみてください。
● たせるかな? たせないかな?
① イヌ 3びき と ネコ 4ひき で なんびきですか?
② バナナ 3本 と エンピツ 2本 で なん本ですか?
③ きんぎょ 2ひき と さば 5ひき で なんびきですか?
④ 100円 と 500円 あわせて いくらですか?
⑤ 2m のひもと 5m のひもを つないだら なんmですか?
⑥ 鉄のパイプ 3本 と アルミのパイプ 5本 があります。パイプは あわせて なん本ですか?
⑦ 3リットルの水と0.2リットルの水をあわせるとなんデシリットルですか?
⑧ 石 3こ と 1円玉 5こ で いくらですか?
⑨ 1円玉 5こ と 50円玉 8こ で あわせていくらになりますか?
⑩ 5リットル の 水の中に 3m の ひもを入れるといくらになるでしょう?
いかがですか? 全問、素直に「たし算」ができましたか? なんだか変…?? という問題も かなりありましたよね。
①は、「3+4=7 答 7ひき」とはしたものの、イヌとネコはたしていいのかな?…と迷います。もし、「動物は あわせて なんびきですか?」と 問われていたらわかりやすいのに。
②は、「3+2=5 答 5本」と出したとしても、この「5本」とはいったい何の数なのでしょう…。「たし算」を初めて習う子どもたちなら、もっと迷うにちがいありません。反対に、平気で「5本」と答えてしまうと、ほんとうにたし算がわかっているわけではないなぁと思ったほうが良さそうです。
子どもにたし算を教えるとき、「こんな方法もあるよ」「これもたしざんなんだよ」とあれこれ一度に教えてしまうと頭の中がゴチャゴチャになってしまいます。
はじめて習うところは、まず 基本の考えをしっかり定着させたい ものです。
例えば「3+2」とは何かを教える場合、まず最初は、
同じものどうしでたし算ができるという ことを押さえます。
初めは具体物を使って実際にやってみせたり、子どもたちにも「たし算」の体験をさせてみてください。その場合、もしアメで教えようと思ったら包装紙も同じ色のアメにしましょう。最初は厳密に同じものどうしにします。
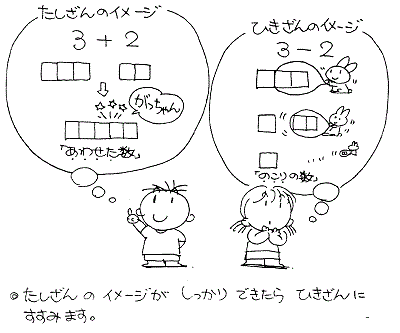
あわせた数を出すのが たし算です。
次のように、①→②→③→④の順番で、たし算を学んでいきます。

① では実際に2こと1このアメを「あわせる」操作をやってみせます。
② ではアメをタイルに置き換えてあわせてみせます。
③ ではたし算の式を教えます。式とは「さんすうの言葉であらわす」ことです。
④ ではたし算の意味を確認します。
ひき算 は、残った数を出す計算 です。
「アメが3こあります。2こ たべました。のこりのアメは なんこですか。」のような問題からひき算を教えるとよいでしょう。最初にあった数から、[ たべたり、あげたり、つかったり、なくしたり、にげたり、帰ったり] していくつか取り除き、その残りを求める場合に ひき算を使います。
ひき算には他にもいろいろな意味があるのですが、上のような「残りを求める」ひき算が子どもたちに最もわかりやすく、操作がしやすいのです。
ひき算の場合も具体物から入って、タイル、式(さんすうの言葉であらわす)だけでできるようにしていきます。
常に「たし算(ひき算)ってどんな数を出すんだっけ?」と、たし算・ひき算の意味を聞いていくのがいいと思います。子どもたちには、今、自分が何をしているのか、何を求めているのかをいつも意識してほしいですね。
②練習順序
★たし算・ひき算 の 練習順序(和が9まで)
あわせた数をだすのが「たし算」 で残った数をだすのが「ひき算」 でしたね。
ところで、たし算はどんなにケタ数が多くなったとしても、「1ケタ+1ケタ」に分解することが出来ますね。このたし算の素になる 1ケタどうしのたしざん のことをたし算の素過程(そかてい)と呼んでいます。
たし算の素過程は、0+0 から 9+9 まで 100個 あります。これはたし算のおおもとのおおもとなので、1つも欠かすことなく教えなければいけません。
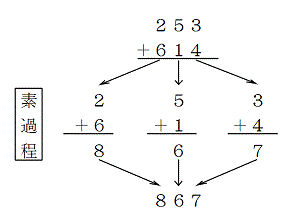
そして、たし算の素過程の逆が、ひき算の素過程(そかてい)になります。こちらも欠かさず教えていきます。
ではまず、たして 9までの「たし算」、つまり、くり上がりのないたし算 について、どんな順序で学ぶと良いかを考えてみましょう。
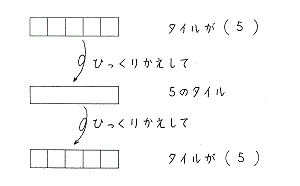
水道方式では、タイル□を使ってたし算を学習していきます。タイル□は5個で「5」のタイルになります。「5」のタイルを使うことで5以上の数が一目でわかります。

2+1 のタイプ はどれだけあるでしょう。書き出してみると、1+1,1+2,1+3,2+1,2+2,3+1
です。これらの式になるような「あわせていくつかな?」という問題を最初にもってきてあげるといいですね。お子さんの大好きな物で楽しい問題を作ってあげてください!
他のタイプも同様に書き出していくと素過程を抜け落ちることなく学習できます。
たして9までのたし算(くり上がりなし)は、
①「5」のタイルを作るかどうか、と、
②「0」が含まれるかどうか、
で型分けし、次のような順序で教えると良いでしょう。
ひき算(くり下がりなし)も、同様に型分けし、次のような順序で教えると良いでしょう。

4-1 のタイプ はどれだけあるでしょう。書き出してみると、 4-1,4-2,4-3,3-1,3-2,2-1です。これらの式になるような「残りはいくつかな?」という問題を最初にもってきてあげましょう。
他のタイプも同様に書き出してみてください。
たし算、ひき算 共に 子どもたちには実際にタイル□ を 操作させて結果を確かめながら計算を進めていきましょう。
さて次は「素過程」の中でも難しい「くり上がりのあるたし算」「くり下がりのあるひき算」です。
③くり上がり・くり下がり は タイルで!
★「10」という まとまり ~ 「10」の合成・分解
私たちがふだん使っている数字は、「十進記数法(じっしんきすうほう)」といって、十集まれば次の位に一くり上がる仕組みです。「9」より1大きい数を1と0を並べて「10」と書くのもそのためです。これによって0~9までの十個の数字だけでどんなに大きな数もどんなに小さな数もあらわせるのでたいへん便利な記数法です。
10以上のものを数えるとき、10ずつまとまりにして数えていくと便利であることはみなさんも経験ずみですね。また「10」をつくるときに、例えば「6」と「4」の組み合わせや「7」と「3」の組み合わせというふうに、私たち大人はたやすく10をつくるためのペアを探し当てることができます。
子どもたちにはこの 「10」の合成・分解 が確実にできるように、タイルと数字で練習してもらいましょう。これが苦手だと、くり上がり・くり下がりの計算がスムーズにいきません。最後には、タイルがなくても数字だけですぐ答えられるくらいまでにしましょう。
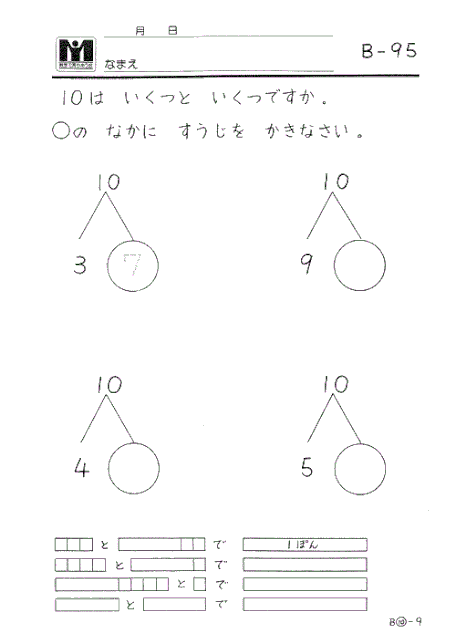
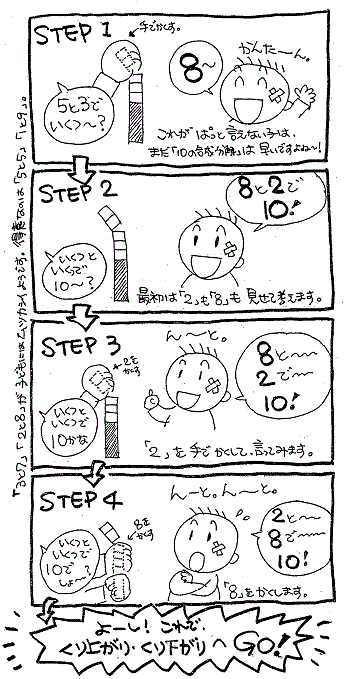
*「10」の合成・分解には、 『10の合成分解タイル』を使おう!
「10」をつくるための組み合わせは全部で 5組 あります。
この組み合わせを練習するために簡単な教具を作ってみませんか。
安価な材料でできて、子どもたちがクイズのようにして学べるので、1つ作っておくと重宝します。
タイルの材料は、木の立方体10個と布製のガムテープ(できればきれいな色で)。接着用にボンド。あとはお子さんの好きなシール(なるべく同じシール5枚)など貼るとかわいいですよ。

★くり上がりのたし算(素過程)
では「1ケタ+1ケタ」(素過程)のたし算で くり上がりのあるもの はどのように考えると良いでしょう。「くり上がり」には、「10のかたまりを作る」 という作業が必要です。
タイルで考えると、「1本」のタイルをつくる ということになります。
※1個のタイル□が10個集まると「1本」のタイルになります。数字の「10」はタイルが1本と0個という意味です。
【タイルの仕組みについて】
8+6の場合
8 は 5 と 3 、6 は 5 と 1 に分解できます。
タイルを置いて考えてみましょう。(下図) 「5」のタイルが両方にあるのでこれらをあわせて「10をつくる」=「1本のタイルをつくる」 ことができます。あとは残りのバラタイルをあわせて答えがでてきます。
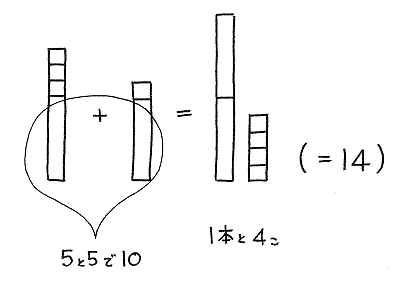
このように両方に5のタイルが含まれていると、5と5で10になるので簡単で理解しやすい方法です。
これと同じタイプは、9+5、7+7、8+7 ・・・ などがあります。最初はこのタイプをタイルで操作しながら練習していくと10のかたまりを作ることが意識できて良いと思います。
9+4の場合
9+4のように、一方が5より小さい場合は、5と5で10のかたまりが作れません。この型では「9にいくつたすと10になるか(10の補数)」を考えさせて答えをだすほうが簡単ですね。
9と1で10が作れるので、4個のタイルから1個をもってくればすみます。 あとはバラタイルが残り、すぐに答えがでてきます。
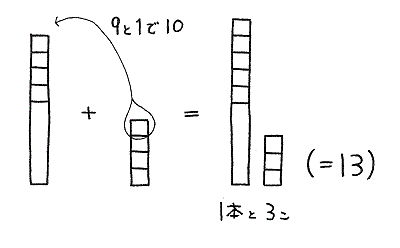
8+3、7+4 なども同じタイプです。
タイルで正しい答えを確かめながら、やがてはたし算の式だけでも答えが出せるまで練習します。たし算の素過程は確実にマスターさせましょう。
「10の合成」が確実にできていると、「8+6」のようなたしざんも10の補数を考えるやり方で良いと思います。
*「いちばんぼし算数数学教室」さんの動画をぜひご覧ください!
数学で育ちあう会の「いちばんぼし算数数学教室」さんが、いろいろな算数教材動画を製作しYouTubeへアップしています。
タイルの勉強や練習ができる動画もありますのでぜひご覧ください。
● いちばんぼし算数数学教室 YouTube
★くり下がりのひき算(素過程)
くり下がりのひき算は、多くの子どもたちがつまずくところです。苦手なまま学年が上がればケタ数が増えてゆきづまってしまうので、素過程のくり下がりは確実にしておきましょう。
ではひき算の素過程で くり下がりのあるもの はどのように考えると良いでしょう。
「くり下がり」には、「10のかたまりをくずす」 という作業が必要です。
タイルで考えると、「1本」のタイルをバラバラにする ということになります。
13-9の場合
13 は 1本のタイルと3個のバラタイルでできています。
一の位の 3 から9 をひくことはできません。
そこで1本のタイルを10個にくずします。10個(5のタイルが1つ+バラタイルが5個)から 9個をとり、残り1個のタイルと3個とを合わせて答えがでてきます。
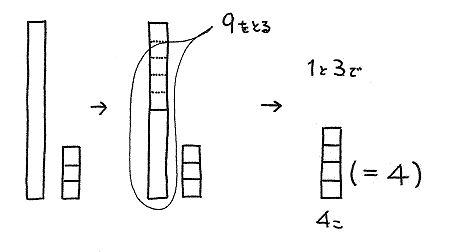
「10の分解」が身についていると、この方法でスムーズにくり下がりが理解できるでしょう。
タイルで正しい答えを確かめながら、やがてはひき算の式だけでも答えが出せるまで練習します。ひき算の素過程も同じく確実にマスターさせましょう。
このようにくり上がり・くり下がりもタイルを使うと、計算の意味を考えながら計算力を習得できます。
たし算・ひき算の素過程(そかてい)は、算数学習にとって基礎中の基礎、これからの土台となっていくものなので、確実にしておきます。
最初は実物を使う、タイルを動かしてみる → タイルを置いてみる → タイルを書いてみる → タイル無しでやってみる、というように少しずつ段階を上げてくり返し学習したいところです。
大事なところはていねいにじっくりと!
④2ケタのたし算・ひき算
★『筆算』を早い段階で取り入れます
現在の小学校算数では、タテ書きの計算=「筆算」 が出てくるのは2年生からです。
でも私たちは、1ケタどうしのくり上がりやくり下がりが出てくる1年生から本来なら筆算を取り入れるべきだと考えます。そのほうが数の仕組みに合っているからです。
教科書においても、数が大きくなれば筆算に切り替えざるをえません。位をそろえなければ、たし算・ひき算ができなくなってしまうからです。それならば早い段階から十進法を意識して筆算を導入していくほうがずっと良いのです。「水道方式」では、位をそろえて書く「筆算」を重視します。
ヨコ書き(暗算)の場合は、そろばんも同じなのですが上の位からたしていきます。筆算は数の仕組みにしたがって下の位から順にたしていきます。
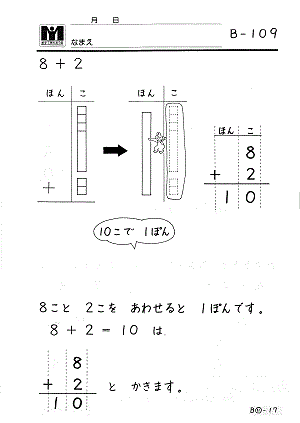
★2ケタのたし算・ひき算
水道方式では、すべての計算問題を型分けします。
【たし算】
最初は2ケタ+2ケタでくり上がりが無い型(例:22+22)から導入し、各位どうしをたし算するという基本をおさえます。それができてから、「0」が入ったり(例:22+20)、位が欠けているもの(例:22+2,2+22)を扱います。
そして次に、くり上がりのあるたし算です。各位をそろえ、下の位から順にたし算をしていきます。
タイルでやってみましょう。
37 + 26
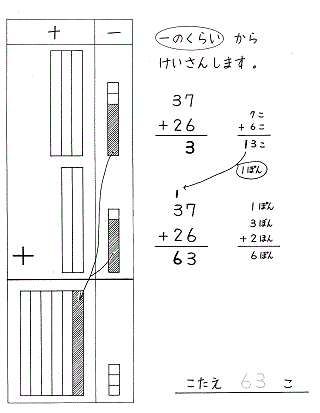
【ひき算】
最初は2ケタ-2ケタでくり下がりが無い型(例:99-22)から導入し、各位どうしをひきざんするという基本をおさえます。それができてから、引く数に「0」が入るもの(例:99-20)、答えに0が入るもの(例:99-29)、位が欠けているもの(例:99-2)を扱います。
そして次に、くり下がりのあるひき算です。各位をそろえ、下の位から順にひき算をしていきます。
タイルでやってみましょう。
33-17
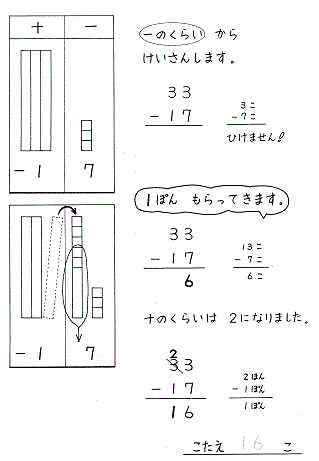
⑤3ケタ以上の計算
★すべての計算問題を型分け
水道方式では、すべての計算問題を 型分け し、「一般型」から「特殊型」へ という順序で教えていくのが大きな特徴です。例えば3ケタのたし算は、教科書などでは、「500+200」のようなものを先に教えます。水道方式では、「123+455」のようなものを先にします。くり上がりがなく、全ての位に0でない数字がある。これを一般型として最初に導入します。
和が3ケタになるたし算は、おおざっぱに書くと次のような順序で学習します。
まず「一般型」をもってきて、各位どうしをたす ということをおさえます。

和が3ケタになるたし算は、おおざっぱに書くと次のような順序で学習します。
まず「一般型」をもってきて、各位どうしをたす ということをおさえます。そして、それぞれの型の中で、例えば、エ.(2回くり上がり) ならば、
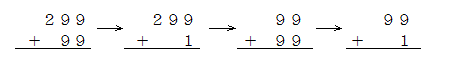
のように「位の欠けているもの」から「答に 0 が入るもの」へと順に学習します。
「0+0=0に決まっているからこれ以上簡単なたしざんはない」というのは大人の思い込み、子どもにはとても難しいのです。
子どもたちは0という数字が出てくると途端にわからなくなりますが、3+5なら安心してたせますね。一ケタどうしのたしざんを、計算の最小のパーツで「素過程(そかてい)」といいました。上のアの型の場合、素過程自体が簡単なので3ケタになっても簡単、それで一般型になったのです。一般型ができればだんだん特殊な型へと流していきます。
ひき算についても同様に分類して、まずくり下がりがない一般型(例:999-222)から入っていきます。
このように型分けをしていると、苦手な型を取り出して練習できるのでとっても効率が良いのです。
3ケタ以上のたし算も各位をそろえ、下の位から順にたし算をしていきます。
タイルで考えれば計算の仕組みを目で確かめ納得できます。
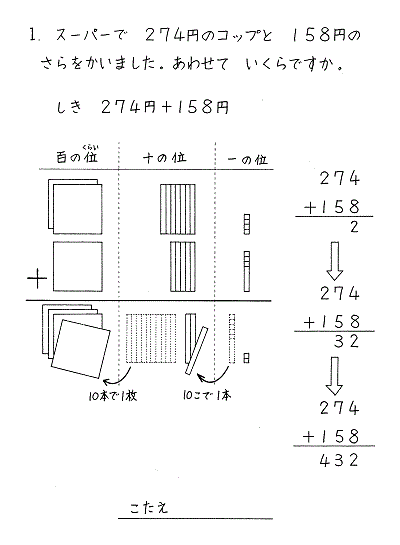
3ケタ以上のひき算も同じようにタイルで学習することで、各位をそろえて下の位から順にひき算をしていけば良いことが理解できます。
*ひき算のまちがい例
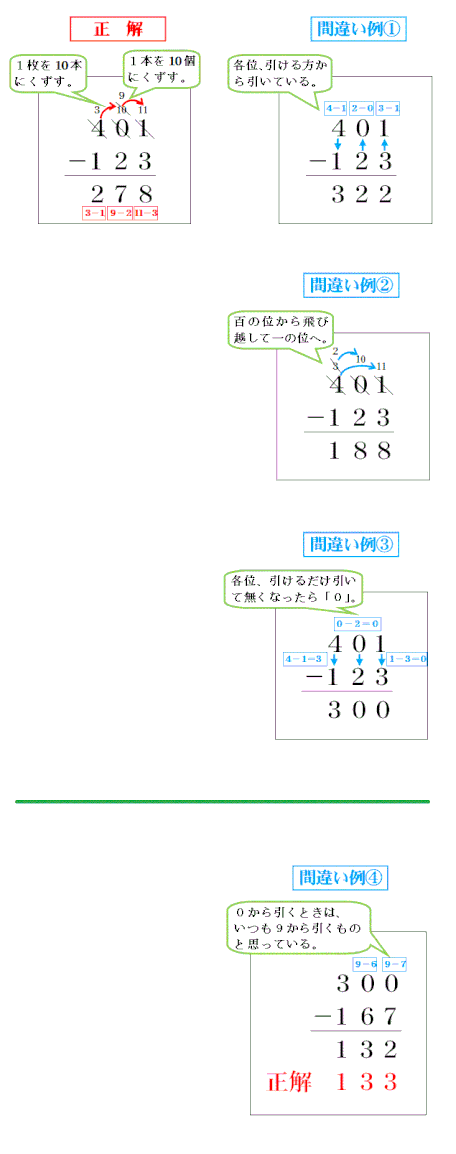
ひき算は苦手な子が多く、3ケタ、4ケタと増えれば、1問解くのに苦労します。子どもたちも大変しんどいところ。ひき算で間違いの多い型が「401-123」や「300-167」のようなものです。
「ひけないので隣から借りようと思ったら0なので、そのまた隣から借りてくる」というパターンの問題です。
また、3ケタまでの計算はバッチリ!!と思っている子どもでも、4ケタのひきざんで次のような間違いをすることがあります。
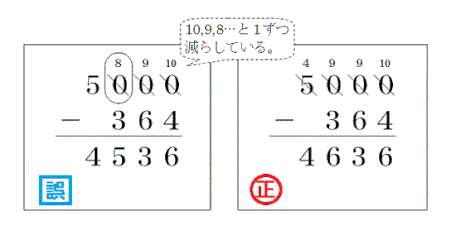
この考えだと、3ケタまでは間違わなかったはずです。でも実は、この子は数の仕組み(十進記数法)がわかっていなかったわけです。
この間違い例でもわかるように3ケタまでの計算では不十分です。4ケタの計算ができるとそれ以上の計算は同じようにできます。いっとき、「ゆとり教育」でなくなっていた4ケタの加減ですが、3ケタができているからといって4ケタも自然とできるわけではないことがわかります。
*「いちばんぼし算数数学教室」さんの動画をぜひご覧ください!
数学で育ちあう会の「いちばんぼし算数数学教室」さんが、いろいろな算数教材動画を製作しYouTubeへアップしています。
タイルの勉強や練習ができる動画もありますのでぜひご覧ください。
● いちばんぼし算数数学教室 YouTube
たし算とひき算の教え方‐2に続きます。
