かけ算の教え方
「かけ算」を「水道方式」ではどのように教えていくのか、教材や資料を例にあげて紹介していきます。
①かけ算の意味
★かけ算の意味は?
小学2年の秋に習う「かけ算」。新しい計算の学習を楽しみにしている人もいますね。「さんいちがさん、さんにがろく、さざんがく…」と「九九」を暗唱するかわいい声が家庭でも聞かれることでしょう。
「かけ算」というと、「九九をいかに早く、まちがいなく言えるか」が焦点となりがちなのですが、実は「かけ算」という演算は、それまで学んだ「たし算、ひき算」とはまったく違う 新しい意味 を持っています。そしてこれが後々、高学年・中学・高校までつながっていくので 「かけ算」は小学校算数のカナメと言えるのです。

そこでまずは かけ算の意味 を考えたいと思います。
かけ算はよく、
「2+2+2+2+2って書くのはめんどうでしょ。でも2×5を覚えたら一発でしょ。覚えようね」
と教えられることがあります。(このように同じ数をたしていくことを「累加」と言います)
けれども最初にこう教えられると、次のような問題が生まれます。
かけ算をたしざんで教えると、かけ算するといつでも増えるのだと思い込んで、後に習う
❶3×0.5=1.5 ←(最初の3より答えは減っている)などの説明がつかない。
❷4×0=4 といった答が多くなる。「4に1回もたさないから4のまま」という発想。
➌同じかけ算なのに小数や分数をかけるときの説明がつかず、計算のやり方だけが押しつけられる。
❹九九だけは早く正確に唱えられるが、文章題ができない。
では、「2×5は、2を5倍すること」 という説明はどうでしょう。
倍は「5倍ズーム」などのように、そのもの自身が拡大するというイメージの強い言葉です。そして、「5倍」の「5」は、目で見ることのできない、操作や関係を表す抽象的な数です。「倍」は2年生にはとらえにくいのでかけ算の導入に適切とは言えません。
それならば「かけ算」をどのように教えればよいでしょう。
数学で育ちあう会では、水道方式の考え方を取り入れ、「かけ算」を身近な題材で導入しています。
その流れをこれからみていくことにしましょう。
②「1あたりの数」×「いくつ分」=「全体の数」
★「1あたりの数」
私たちのまわりには、1つのものに同じ数だけあるもの、例えば、ネコの耳は二つ、のように数が決まっているものがたくさんあります。それを「ネコ1ぴきあたり耳2つ」というふうに表します。これが「1あたりの数」です。もしネコが3びきいたら、耳の数は全部で、「2つ×3=6つ」です。
トンボのはねは「1ぴきあたり4枚」です。トンボが7ひきいたら、はねの数は全部で、「4枚×7=28枚」です。
こんなふうに、子どもたちの身のまわりのものから、「1あたりの数」をたくさん探してみましょう。
生き物以外の人工物の場合も、
「自動車1台あたりタイヤ4本、5台作ればタイヤは全部で何本?」
のように言えて、「4本×5」から全体の数が出てきます。
また、下の問いのような
「おにぎりを1人に2こずつ、4人にくばる」
という場合も「1あたりの数」が決まるから、「2こ×4」で全体の数が求められます。
このように、
「1あたりの数」がいくつあるかで全体の数がわかる計算を 「かけ算」 といいます。
「1あたりの数×いくつ分=全体の数」という考え方です。たし算やひき算とはまったく違う、新しい演算である「かけ算」の概念が、具体的な場面をたくさん考え、実際に操作をして体験を重ねることにより、子どもの頭の中で整理され、理解されていくのではないでしょうか。
数学で育ちあう会が各地で開催している「お母さんの算数教室」でも、かけ算を次の絵のように、ピカチュウの耳の数を尋ねた問題で意味を考えていきます。

どのピカチュウにも耳が2本ずつ有ります。これを「1あたりの数」ということにします。
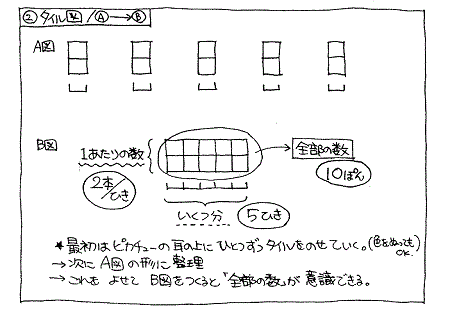
そして、これらをタイルで表します。タイル□はお耳、お皿はピカチュウを表しています。2本/ひきで5ひきいるとき、お耳の数は全部で何本ですか。10本ですね。
ここでも「タイル」が視覚的に大切な役目を果たしています。
タテに積まれたタイルの数が「1あたりの数」に、下側のお皿が「いくつ分」になり、かけ算するとタイルがピタッとくっつきます。そのタイルの数が「全体の数」となるのです。
このようにタイルでかけ算を表せることを知っていれば、九九を忘れたときにもタイルを書いて答を出せるわけです。
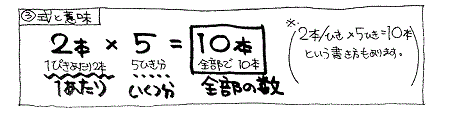
かけ算は「×(かける)」の記号を使って式を作ります。子どもたちは、たくさんの具体的な場面を与えられ、そのたびに手を動かして具体物やタイルを使って結果を得ます。
そのことを日本語で話し、そして、さんすうのことばに置き換える→「式」を作ることができるようになってほしいのです。

こうしてかけ算の意味をしっかり学習してから、「九九のうた」に入っていきます。九九のうたをおぼえるときも、それぞれの「段」で、代表的な「1あたりの数」をあげながら、タイルや式と関係づけて覚えられるようにしています。
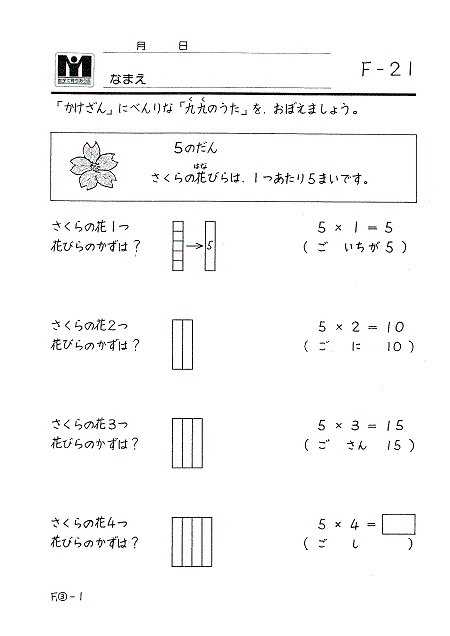
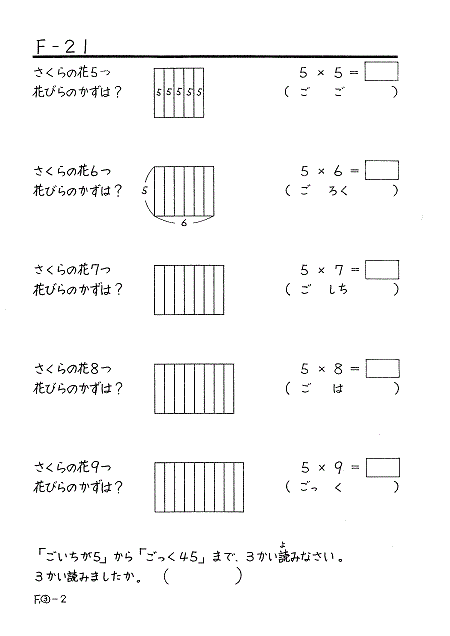
このように「かけ算」が「1あたりの数×いくつ分=全体の数」であることを学ぶと、もし九九を忘れたとしても、かけ算のタイル図を描けばその九九の答を出すことができます。
子どもたちには、1あたりの数が「0」という場合も考えさせます。「かえるのおへそ」は1ぴきあたり0個、「生まれたばかりの赤ちゃんの歯」は1人あたり0本、などなど。
学校の教科書ではかけ算九九は小学2年生で、0を含むかけ算は小学3年生で扱っています。数学で育ちあう会では、かけ算の意味を十分理解してもらうためにも、2年生でまとめて学習させています。

かけ算のタイル図では、「1あたりの数」が増えればタイルが上へ上へといくらでも伸びていき、「いくつ分」が増えれば横に横にと果てしなく広がります。かけ算とは、上にも横にも広がりを持つ演算であることが、子どもたちにもなんとなく感じとれるのではないでしょうか。
このようにかけ算の意味がわかっていると、高学年で出てくる「単位あたり量」(密度、速さ、濃度など)の理解がスムーズになります。
「かけ算」の意味がわかっていなければ 「わりざん」 もわからないし、正比例・反比例をはじめとする関数や、割合などの理解も困難です。九九を覚えればかけ算の勉強はおしまいではなく、かけ算の意味こそ時間をかけて、ていねいに教えなければならないと私たちは考えています。
そして、生活や遊びを通して、一つのものに同じ数だけあるものを自然に取り込んでいけば、かけ算の理解もより深まるのではないでしょうか。
*教え方のポイント! もしお家で「1あたりの数」を教えるなら…
お菓子を使ってみるのも、子どもたちが喜ぶ方法です。
市販のお菓子で、例えば、1箱に2個入っているキャラメルとか、1袋4枚入りのビスケットとか、1つ9枚入りのガムだとか…。駄菓子屋さんで探してみても楽しいですね。

*「いちばんぼし算数数学教室」さんの動画『算数教材動画』をぜひご覧ください!
数学で育ちあう会の「いちばんぼし算数数学教室」さんが、いろいろな算数教材動画を製作しYouTubeへアップしています。
タイルの勉強や練習ができる動画もありますのでぜひご覧ください。
● いちばんぼし算数数学教室 YouTube かけ算①
https://youtu.be/MOmff-0RII0?feature=shared
● かけ算②
③かけ算の筆算 〈その1〉
★『筆算』を早い段階で取り入れます
現在の小学校算数では、2年生の2学期にかけ算と九九を学習し、3学期には「4×12」のようなものを例えば「4×9」と「4×3」に分解してから合わせるという方法で扱っています。けれど、かけ算のタテ書きの計算=「筆算」 が出てくるのは3年生になってからで、2ケタ×1ケタでようやく筆算を取り入れています。
私たちは「1ケタ×1ケタ」の段階から筆算を取り入れるべきだと考えます。
かけ算の計算で大事なのは、位ごとにかけて位ごとに合わせることです。筆算ならケタ数が増えても位をそろえて計算できる のです。
私たちは、九九のうたを覚えた後にかけ算の筆算を導入しています。

★2ケタのかけ算の筆算もタイルで納得!
2ケタのかけ算、例えば「12×4」などは、タイルで計算のしくみを説明するとよくわかります。
【もんだい】
12こ入りのキャラメルの箱が、4箱あります。キャラメルは、全部でなんこありますか?
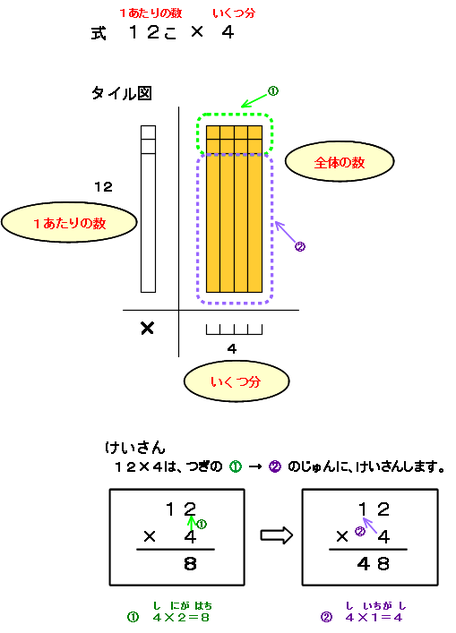
キャラメル1箱あたり12個入っているので1あたりの数は12個(タイル1本と2こ)です。これが4箱分になるので、式は
12×4 になります。
タイル図で表すと上図のようになりますね。これを筆算の計算と結びつけて考えます。
1の位から順に、かける数「4」の段の九九を使って計算します。
①まず4×2を計算します。
4×2=8(こ)→タイル図では、緑色の点線で囲んだ①の部分になります。
②次に4×1を計算します。
4×1=4(本)→タイル図では、紫色の点線で囲んだ②の部分になります。
あわせると、
4本と8こになって、答は48 です。
12×4=48 こたえ 48こ
かけ算の筆算の大原則は
★位ごとにかけて合わせる ことです。
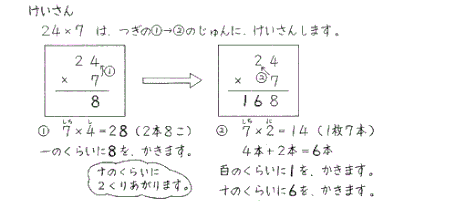
次のように、かけ算した結果くり上がる場合も、同じタイルどうしを合わせます。そしてタイル10こで1本に、タイル10本で1枚にしてまとめていけばよいわけです。
※タイル10こ=1本 に、 タイル10本=1枚 になります。
タイルの数の仕組みについては【数の教え方】の「十進記数法」とタイルをどうぞ。
④ かけ算の筆算 〈その2〉
★「2ケタ×2ケタ」の筆算もタイルで「なるほど!」
かける数が2ケタになっても、タイルで計算のしくみを表すと、どの部分で何を求めているかの説明がつきます。では、「12×23」を例にとって見ていきましょう。
【もんだい】
12こ入りのキャラメルの箱が、23箱あります。
キャラメルは、全部でなんこありますか?

12×23=276 こたえ 276こ
上のタイル図でわかるように、最後に同じ種類のタイルどうしをたし算します。そのためには筆算で位をそろえる必要があります。左に一つずつ位をずらして書くのは同じ種類のタイルどうしでそろえているからなのです。
※実際に子どもたちを指導する場合は、この図の前に「3×10」や「10×10」などをタイルで表すとどうなるかを学習しています。
かけ算の筆算の大原則は
★位ごとにかけて合わせる でした。
ここに十分気をつけながら「×3ケタ」まで進んでかけ算の課程が修了します。
ちなみに学校の教科書では、3年生で「×2ケタ」までを習って、4年生で「億」を習ってから「×3ケタ」を学習しています。
★タイルは、後々まで重宝する「数学の道具」なのです!
これまで見てきたようにタイルでかけ算のしくみを学ぶと、かけ算が「1あたりの数×いくつ分=全体の数」ということがイメージしやすくなります。この考え方はあとで習う「わり算」や「単位あたり量」などにもたいへん重要です。また長方形・正方形の面積はかけ算のタイル図が発展的に生かされることになります。
そして、タイルの良さは小学校の算数にとどまりません。中学数学にも高校数学にもつながるとっても便利なものなんです。
ひとつ例をあげると、中学で出てくる「因数分解」と「展開」です。タイルだとこんなふうに表せます。
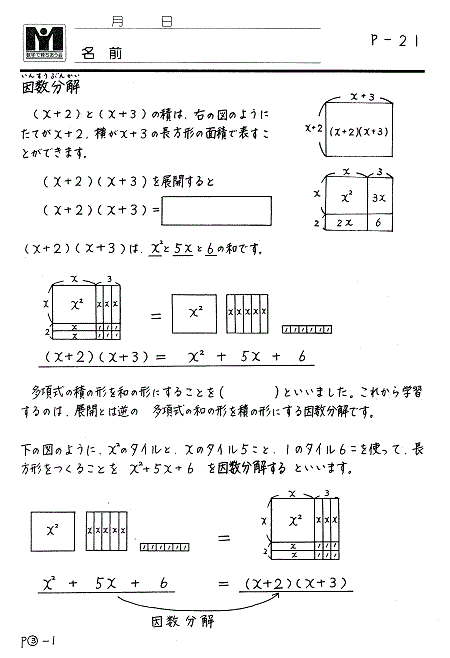
中学で習ったときは何をやっているのかよくわからなかった因数分解が、タイルをパズルのように並べ替えてかけ算の形に直すことだったなんて驚きですね!
「タイル」は、数学のいろいろな分野に登場する「かけ算」を、図に表すことができる重宝な道具です。
タイルがイメージ図となって子どもたちの思考を助けてくれることと思います。
